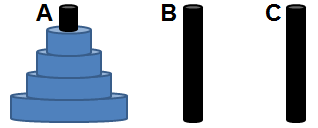
Existen varias versiones y variantes del problema de las torres de Hanoi, pero la versión clásica y más común es la siguiente:
Se tienen tres postes, normalmente denotados como A, B y C, y en uno de ellos (poste de origen, usualmente A) se tienen apilados n discos de diferentes diámetros.
El problema consiste en pasar los n discos del poste origen al poste destino (usualmente C) manteniendo en todo momento las siguientes reglas:Ahora bien, para el caso de n = 1, si A es el poste origen, C el poste destino, y B el poste auxiliar, la solución es directa:
- Sólo se puede mover un disco cada vez.
- Un disco de mayor diámetro no puede estar sobre uno de menor diámetro.
- Sólo se puede mover el disco que se encuentre en la parte superior de cada poste.
Mover el disco 1 del poste A al poste C.
Para el caso de n = 2, si A es el poste origen, C el poste destino, y B el poste auxiliar, la solución está dada por los siguientes movimientos de discos, donde el disco 1 es el más pequeño y el disco 2 es el más grande:
Mover el disco 1 del poste A al poste B
Mover el disco 2 del poste A al poste C
Mover el disco 1 del poste B al poste C
Para el caso de n = 3, si A es el poste origen, C el poste destino, y B el poste auxiliar, la solución está dada por los siguientes movimientos de discos, donde el disco 1 es el más pequeño y el disco 3 es el más grande:
Mover el disco 1 del poste A al poste C
Mover el disco 2 del poste A al poste B
Mover el disco 1 del poste C al poste B
Mover el disco 3 del poste A al poste C
Mover el disco 1 del poste B al poste A
Mover el disco 2 del poste B al poste C
Mover el disco 1 del poste A al poste C
Para visualizar mejor la solución, se sugiere como ejercicio realizar los dibujos que reflejen la naturaleza de estos movimientos. Adicionalmente, se sugiere realizar la misma labor para cuatro y cinco discos. Hágalo antes de continuar.
Si realizó lo sugerido en el párrafo anterior, quizá haya identificado algunos patrones:
Si realizó lo sugerido en el párrafo anterior, quizá haya identificado algunos patrones:
- Para el caso de cuatro discos, se tiene la situación inicial sugerida por la siguiente figura:
- Para el caso de cuatro discos (en general para el caso de n discos), después de algunos movimientos se tiene la situación presentada en la siguiente figura, en la que se observan los n - 1 discos colocados en la posición auxiliar B, y el disco de mayor diámetro listo para ser movido a su posición final:
- El siguiente paso es el movimiento del disco de mayor diámetro de la posición origen A hacia su posición final de destino (C). Observe que los discos en la posición auxiliar no se afectan, como lo muestra la siguiente figura:
- Ahora bien, de la figura anterior puede notarse lo siguiente: en la posición B están los n - 1 discos restantes, es decir, el problema original de n discos pero simplificado (al menos por un disco), por lo que, si se toma como nuevo origen la posición B, se mantiene el destino en la posición C y se hace que la posición auxiliar sea ahora A, se tiene la misma situación del problema original pero con menos discos y con nuevos roles respecto a la posición de origen y la auxiliar.
En resumen el problema se reduce ahora a mover los n - 1 discos de la posición B a la posición C utilizando a la posición A como auxiliar, y si se repite el procedimiento, se obtendrá eventualmente la situación presentada en la siguiente figura:
De lo anterior se pueden deducir las relaciones de recurrencia y el caso base para dar solución recursivamente al problema de las torres de Hanoi. De manera general, se presenta a continuación el algoritmo de las torres de Hanoi:
Algoritmo mover_disco(n: entero, origen: character, destino: character, auxiliar: character)
Inicio
if (n == 1)
imprimir mover el disco n de la posición origen a la posición destino
else
mover_disco(n - 1, origen, auxiliar, destino)
imprimir mover el disco n de la posición origen a la posición destino
mover_disco(n - 1, auxiliar, destino, origen)
end if
Fin
Observe que el algoritmo anterior es una descripción en pseudo código de los patrones identificados en el texto. Por otro lado, si se realizó el ejercicio sugerido con anterioridad, un análisis cuidadoso deberá llevar al lector a la identificación de dichos patrones.
Consideraciones adicionales.
En resumen, las implementaciones recursivas son en general ineficientes en tiempo y espacio, pero muy elegantes y simples una vez que se tiene identificada la relación de recurrencia. En este sentido, siempre que pueda identificar un enfoque iterativo que sea sencillo de implementar, opte por él.
Por otro lado, el problema de las torres de Hanoi es un ejemplo ineludible de que por medio de la recursividad es posible solucionar problemas complejos de manera bastante sencilla, aunque el precio a pagar sea la eficiencia en tiempo y espacio de memoria. Intente resolver el problema de las torres de Hanoi de manera iterativa para tener una mejor comprensión de lo anterior, y experimente directamente y de primera mano el eterno conflicto (tradeoff) computacional entre espacio vs. tiempo, y eficiencia vs. simplicidad.
Por otro lado, el problema de las torres de Hanoi es un ejemplo ineludible de que por medio de la recursividad es posible solucionar problemas complejos de manera bastante sencilla, aunque el precio a pagar sea la eficiencia en tiempo y espacio de memoria. Intente resolver el problema de las torres de Hanoi de manera iterativa para tener una mejor comprensión de lo anterior, y experimente directamente y de primera mano el eterno conflicto (tradeoff) computacional entre espacio vs. tiempo, y eficiencia vs. simplicidad.